円周率計算

下記のソースコードは，モンテカルロ法によって円周率の近似値を求めるためのプログラムです．

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define N (100 * 1000 * 1000)

static struct timespec diff(struct timespec start, struct timespec end)
{
    struct timespec ts;

    if (end.tv_nsec - start.tv_nsec < 0) {
        ts.tv_sec = end.tv_sec - start.tv_sec - 1;
        ts.tv_nsec = 1000000000 + end.tv_nsec - start.tv_nsec;
    } else {
        ts.tv_sec = end.tv_sec - start.tv_sec;
        ts.tv_nsec = end.tv_nsec - start.tv_nsec;
    }
    return ts;
}

static void compute()
{
    // 原点を中心とする半径1の円に含まれる点の個数
    long long count = 0;

    double x, y;
    struct drand48_data buffer;
    struct timespec ts;

    // 疑似乱数生成器を現在時刻で初期化
    clock_gettime(CLOCK_MONOTONIC, &ts);
    srand48_r(ts.tv_nsec, &buffer);

    // 計N個の点を生成する
    for (int i = 0; i < N; i++) {
        // [0, 1)の範囲の乱数を生成し，xとyに代入
        drand48_r(&buffer, &x);
        drand48_r(&buffer, &y);

        // (x, y)が原点を中心とする半径1の円に含まれるなら
        if (x * x + y * y < 1.0) {
            // countを1増やす
            count++;
        }
    }

    // 円周率の近似値を表示
    double pi = 4.0 * count / N;
    printf("estimated pi = %lf\n", pi);

    // 近似値の真値からの誤差を表示
    printf("error = %lf\n", fabs(pi - M_PI));
}

int main(int argc, char *argv[])
{
    struct timespec start_ts, end_ts;
    clock_gettime(CLOCK_MONOTONIC, &start_ts);

    compute();

    clock_gettime(CLOCK_MONOTONIC, &end_ts);

    struct timespec elapsed_ts = diff(start_ts, end_ts);

    printf("elapsed:    %ld.%09ld [s]\n", elapsed_ts.tv_sec,
           elapsed_ts.tv_nsec);

    return 0;
}

具体的なアルゴリズムは次の通りです． 1x1の正方形内にランダムに点を打ち，半径1の円の中に含まれる点の個数を数えます． 円に含まれるの点の数を全ての点の数で割ると，4分の1円の面積の近似値が求まります． これを4倍すると，円周率の近似値が得られます．上の例では， 10億個の点を打っています．

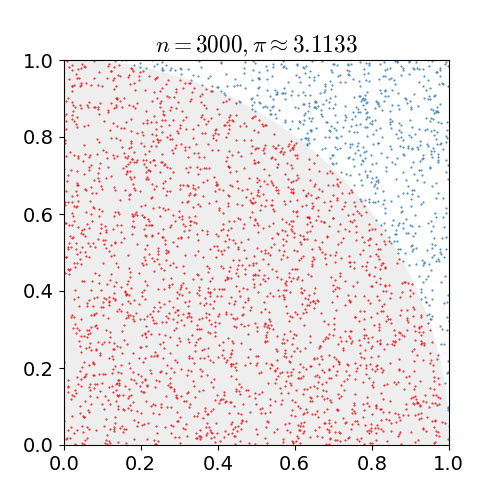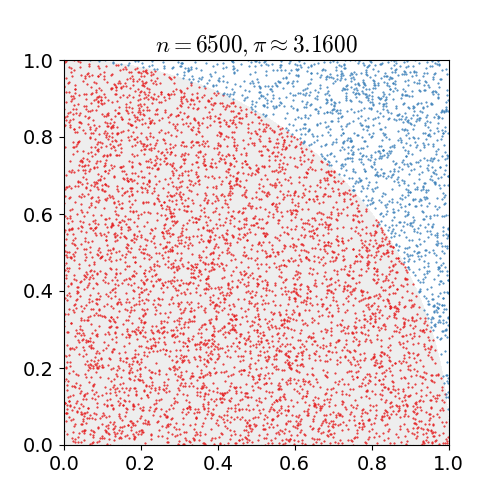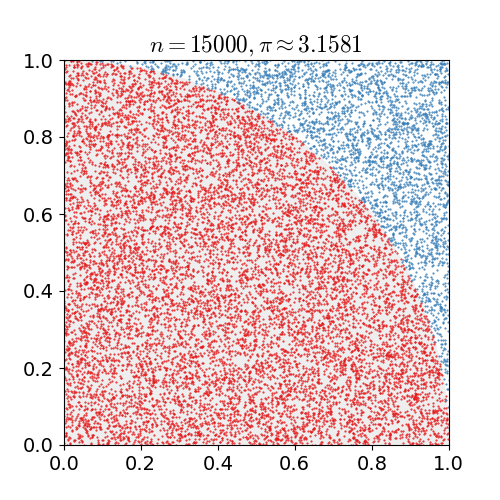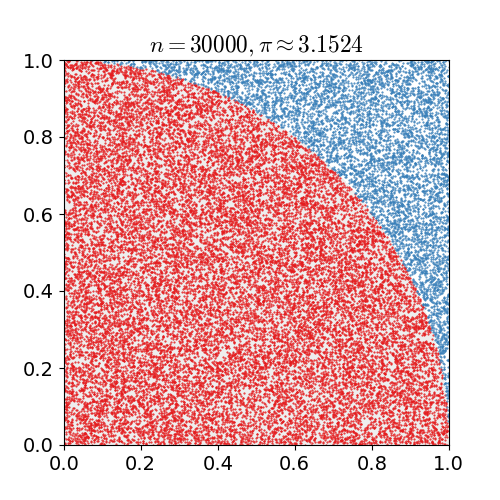nicoguaro CC BY 3.0

やってみよう

• このプログラムをノード内並列化してみましょう．
• このプログラムをノード間並列化してみましょう．